definition of quantum mechanics in chemistry

Definition of Quantum Mechanics Introduction

Classical mechanics does not provide an accurate description of matter on the scale of atoms and molecules. Electrons around a nucleus or nuclei do not behave like planets orbiting the sun or like ping-pong balls bouncing around in a container. Experiments show that when observing the properties of very small bits of matter, such as a single electron, the matter exhibits wave-like properties. Quantum mechanics is the mathematical description of matter on the atomic scale.

In chemistry we are mostly interested in the electrons that give atoms their properties and hold atoms together to form molecules. Thus to describe matter, and to predict the properties of molecules, we must use quantum mechanics . Terminology

• operator - a series of mathematical steps.
• Hamiltonian,  - the operator that describes the energy of an electronic system.
• wavefunction, 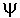 - a mathematical function that describes a wave-like shape.
• eigenvalue - a value obtained from operating on a wavefunction.

The behavior of a quantum particle is completely described by the Schrödinger equation:

A given Hamiltonian operator will have a series of wavefunctions that satisfy the Schrödinger equation. These wavefunctions are called eigenfunctions. The Hamiltonian operating on the eigenfunctions produces the eigenvalues, E, which are the allowed energies of the system.

For an illustration of how to use the Schrödinger equation see the one-dimensional particle-in-a-box.